- 本篇文章是我第一次读树结构相关的内容,难度较大数学概念有点多,我尽量讲清楚
- 关于树拓扑结构的重建,现有方法可分为两大类:基于分割的方法和基于骨架的方法。
- 基于分割的方法高度依赖于输入数据的质量,因此对于存在质量问题的数据,如异常值或因闭塞而缺失的数据,可能不够稳健
- 另一些基于骨架的方法则主要基于规则,高度依赖用户的输入和参数调整,比较麻烦,本文的方法主要基于骨架
Materials and Methods
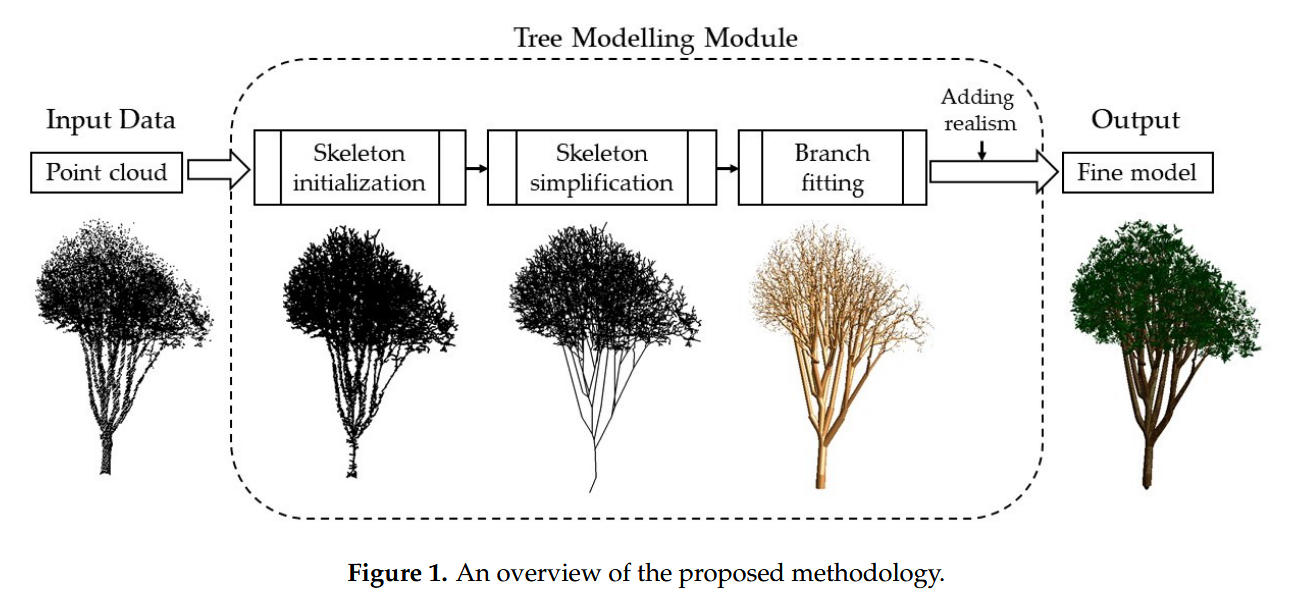
Skeleton Initialization
- 在这个骨架初始化的阶段,我们的大框就是用MST图来构建树的骨架
- 首先对于初始输入的点云,如何构建MST图呢?
- 首先,采用Delaunay triangulation把初始点云,变成三角剖分图,这里包含这个边和点。
- 这里的Delaunay triangulation,就是让平面上一组点连成三角形的方法(不重叠,覆盖全部,在某个三角形的外接圆内,只包含在外接圆上的三个节点,不包含其他节点)
- 其优点:生成的网格较为均匀,不仅可以解决点缺失的问题,还在寻找最短路径的问题中非常的高效
- 德劳内三角形生成算法 Delaunay triangle generation algorithm(I)_哔哩哔哩_bilibili
- 之后我们为图的每条边要分配权重,为了后面的Dijkstra shortest path algorithm做准备
- 用Dijkstra shortest path algorithm以树根为起点的最短路径树,作为个体树的初始骨架表示
- 总结:初始点云--Delaunay triangulation-->三角剖分图--Dijkstra shortest path algorithm-->初始骨架
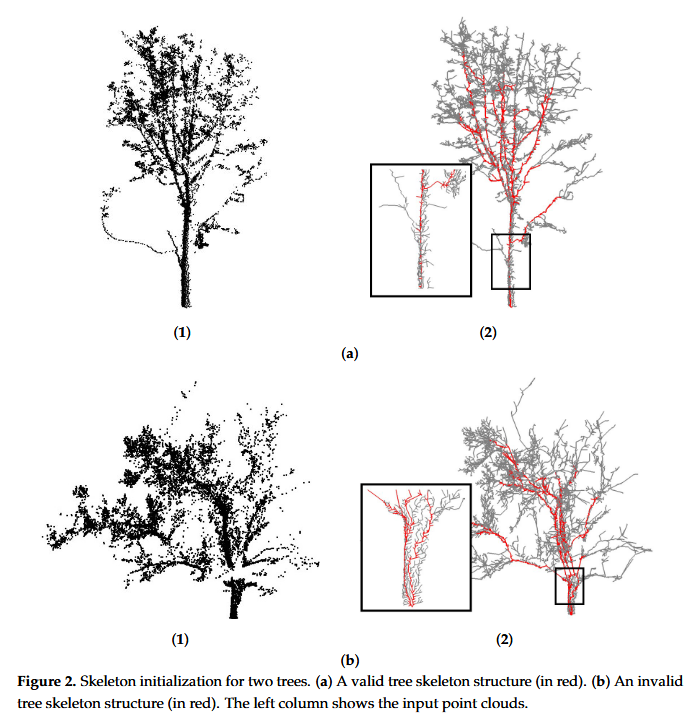
- 存在问题:有的树比较矮短有分散的点,右侧生成的骨架就容易水平长
- 解决方式:将属于树的主要分支的点集中起来
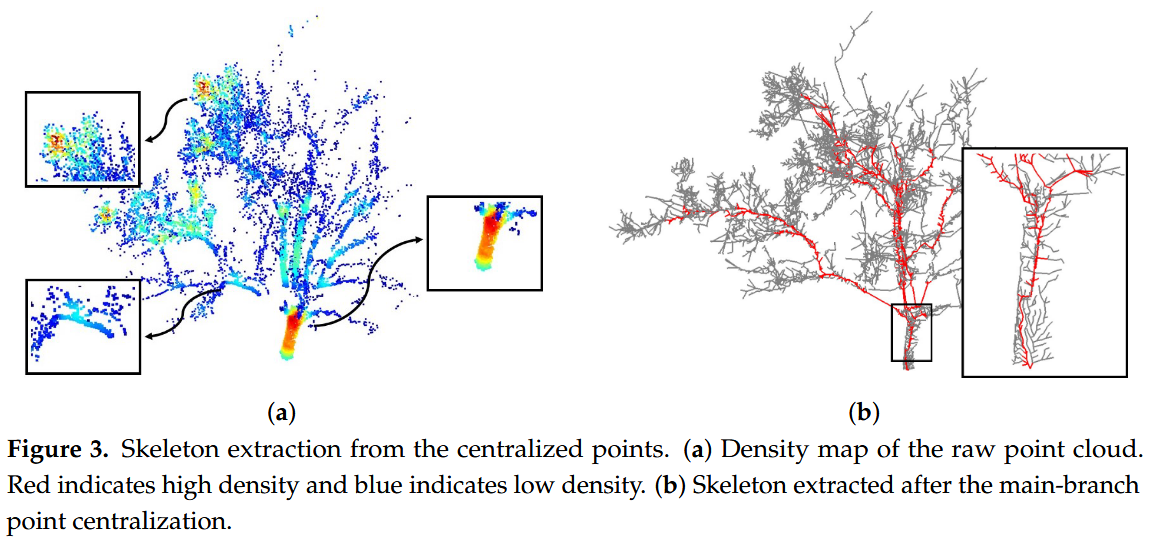
- 分叉点或分支顶端附近的点密度经常会发生急剧变化,而单个分支内的点密度较为稳定,我们可以找到主分支点,因为它们的邻近点密度相对稳定。通过均值移动算法将识别出的主枝点集中起来。如图 3b 所示,主支点集中化后提取的骨架具有紧凑的垂直生长方式
- 均值移动:对每一个点,在其邻域内计算密度的均值方向(即移动方向),不断迭代地移动该点朝向密度更高的区域,直到收敛到密度最大值(模式中心)
Skeleton Simplification
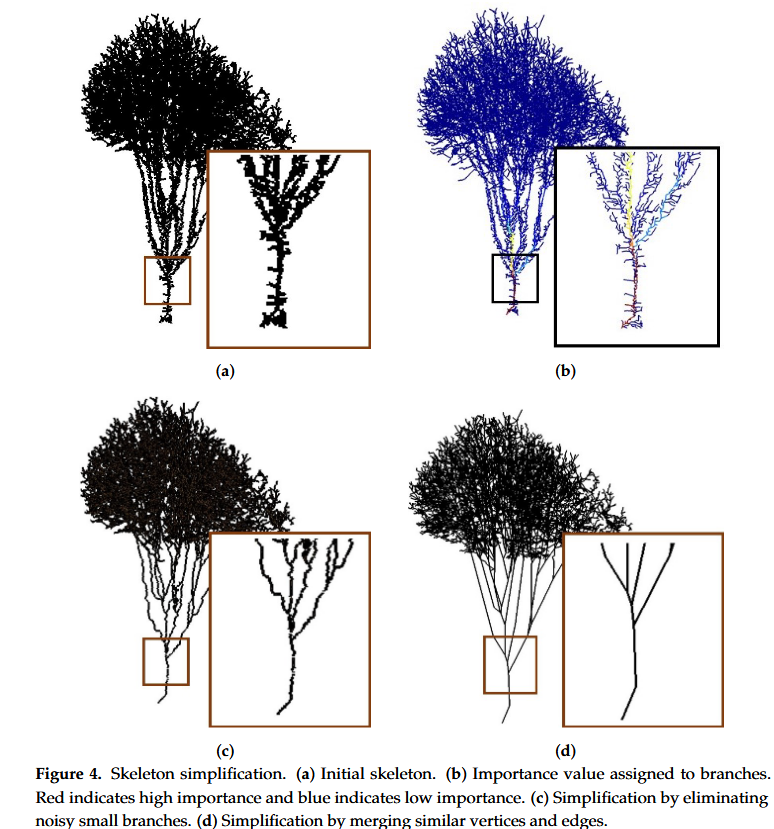
Assigning Vertex and Edge Importances
- 在这个阶段,我们的目标是保留重要顶点和主分支边,同时忽略短分支和噪声点
- 首先排除了以往研究中使用过的一种方法,即根据点的局部密度或通过主成分分析(PCA)提取的法线来判断重要性。他们认为这种方法过分依赖于点云的扫描质量,在数据质量差的情况下结果不可靠
- 点的局部密度:在一个点的邻域内,统计点的数量或分布情况。假设一个点的邻域中点非常稠密,可能意味着这个点处在结构的核心区域或特征区域。密度较低的点可能是边缘、稀疏区域,或者噪声点。
- PCA:找出数据主要变化方向,计算邻域点协方差矩阵的特征向量,最小特征值对应的特征向量,通常被认为是法线方向,通过法线方向、曲率等信息,判断该点是否处在结构变化区域。
- 本文的方法:
- 定义:对于骨架中的任意一个顶点
v,它的子树被定义为v自身以及所有由它延伸出去的后代顶点和边 。简单来说,就是一个顶点以及从它开始生长出去的所有分支部分。 - 一个顶点
v的重要性值:被计算为其子树内所有边的长度之和- 这样,靠近树基区域的高连接顶点权重较大,而靠近树冠的低连接顶点权重较小。
- 边的权重计算规则:一条边的重要性,是由它连接的两个顶点的重要性(即各自的子树长度)的平均值来决定的
- 位于树顶的末梢小树枝,它们的权重都普遍较低且比较一致
- 在靠近树根的区域,主干部分的权重会极其高,而旁边因扫描错误产生的孤立小“噪声”分支,其权重会极其低。这两者之间形成了巨大的权重差距。
Simplifying Adjacent Vertices and Edges
- 再上一个部分我们已经剔除了一些不重要的分支(比如主干附近的噪声点)
- 为了,我们定义了一个相似性指标 α 来描述目标顶点之间的接近程度
- 对于拥有单个子节点的顶点:其实可以转变成线段简化问题,采用的方法是Douglas-Peukcer算法
- Douglas-Peukcer算法是一种精简的算法,处理大量冗余的几何数据点,既可以达到数据量精简的目的,有可以在很大程度上保留几何形状的骨架
- 3.多边形曲线简化之Douglas-Peucker算法_多边形简化-CSDN博客
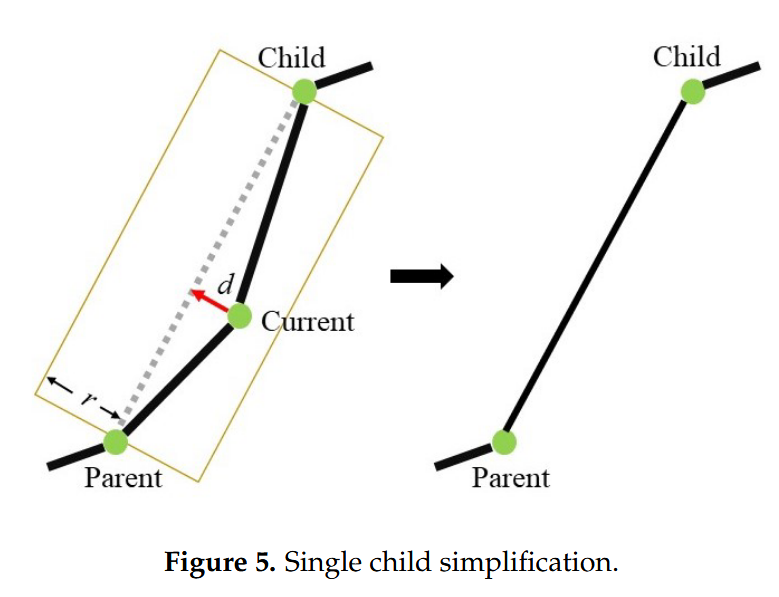
- 当前顶点距离其父节点和子节点所形成的线段越近,该顶点就越不重要,当该距离小于阈值我们可以把这个点去掉
- 我们计算这个指标 α 的时候定义 α= d/r ,其中 r 是树状骨架中边的距离阈值,用于控制简化过程如果 α ≤ σ 的时候把点去掉
- 对于拥有多个子节点的顶点:相似性指标 α 被用来评估其子节点之间的接近程度。
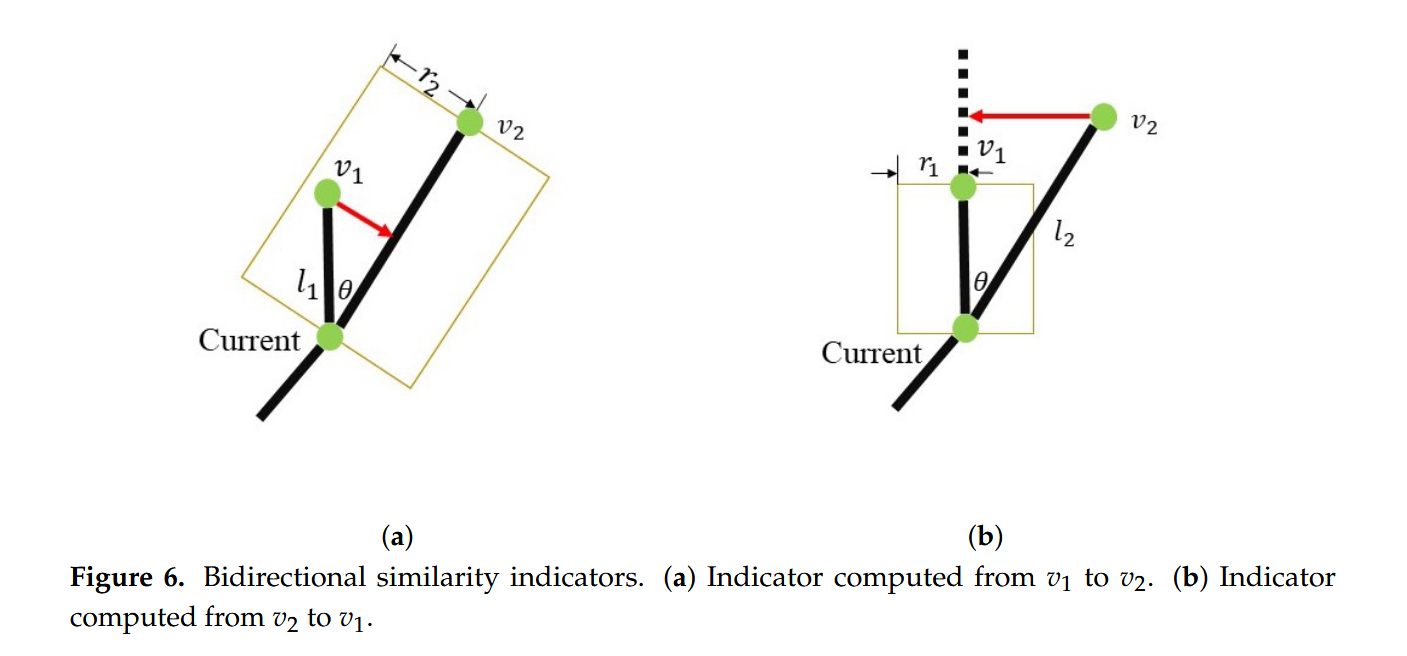
-
\alpha = \min\left(\frac{l_1 \sin \theta}{r_2}, \frac{l_2 \sin \theta}{r_1}\right)
- 其中,l 表示特定子顶点与其父顶点之间的边长;θ 表示两条边之间的角度,r 表示特定边的距离阈值,可以看到我们的v1->v2还是v2->v1的值不一样,取最小值做指标值如果该指标小于阈值,把二者合并一个新点
- 合并后的新顶点位置计算为原始两个顶点的加权平均值
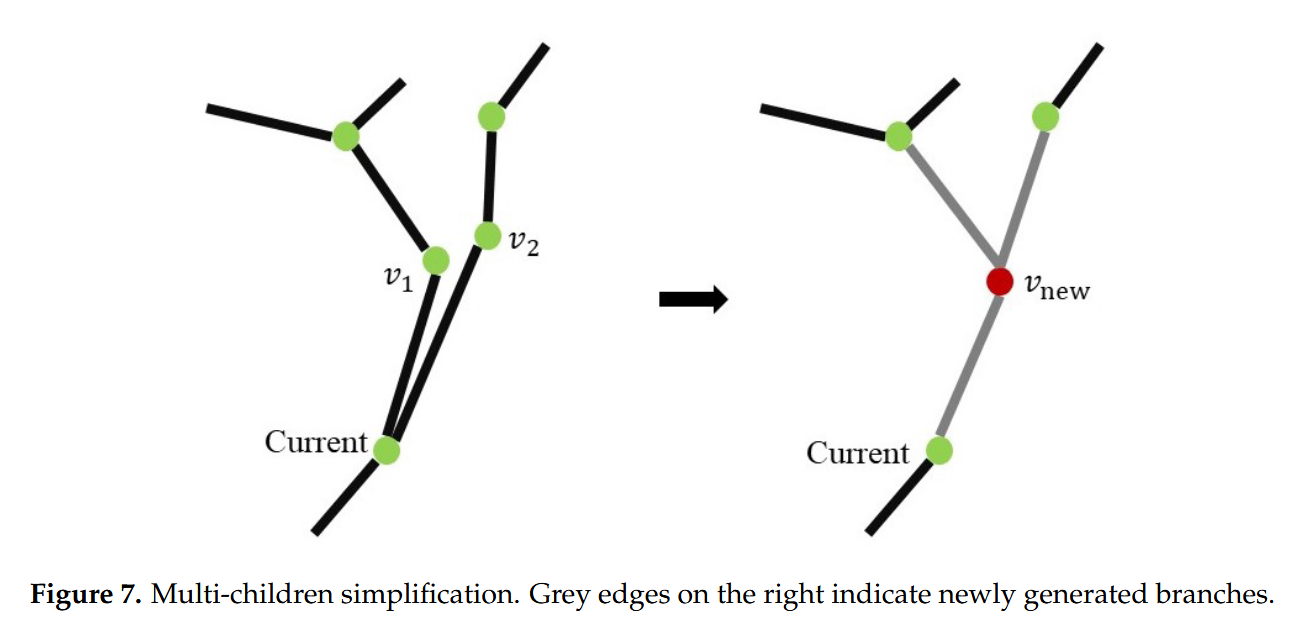
-
p_{new} = \frac{p_1 w_1 + p_2 w_2}{w_1 + w_2}
- 新顶点的位置是根据原始两个顶点的权重(即它们的子树长度)计算出的加权平均值。
- 合并后,原先连接到旧顶点的邻里关系会自动更新,从而在局部操作中保持整体树木结构的完整性。
-
Branch Fitting
- 我们拿到了简化版本的骨架,之后为了精确地模拟树枝的几何形态,算法采用了一种cylinder-fitting approach(圆柱体拟合)的方法 。即使数据集中存在孔洞和噪声,圆柱体在表示树枝几何方面也是最稳健的基本形状
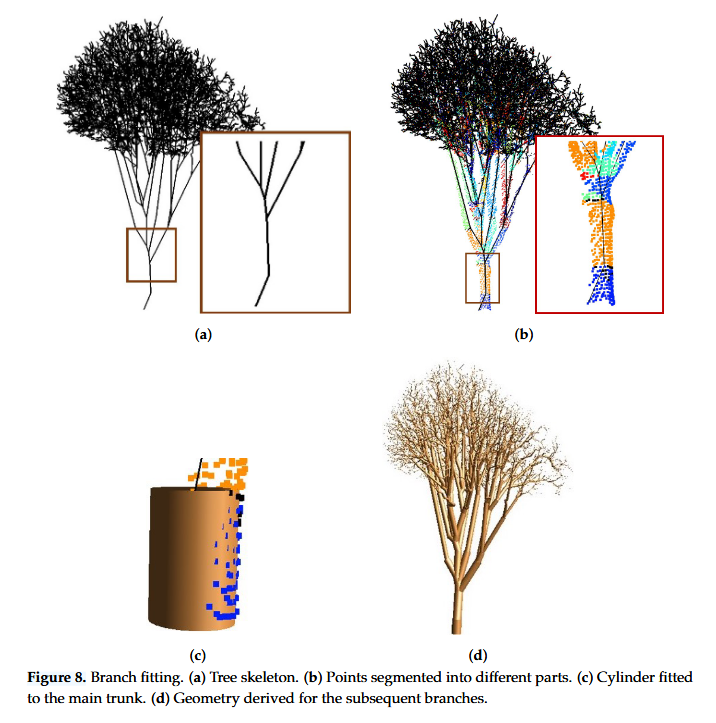
- 由于树的基部密度比较大,采用基于优化的方法
- 识别点云:首先,算法会分割并识别出属于主树干部分的邻近点云 。
- 非线性最小二乘法拟合:接下来,算法将一个圆柱体与这些树干点云进行拟合 。这被定义为一个典型的非线性最小二乘法问题 ,其目标是求解圆柱体的参数,使得所有相关点到圆柱体表面的平方距离之和最小 。
- 输入数据:输入点的位置 p 。
- 待解参数:圆柱体轴线的方向向量 a、轴线上端点的位置 p_{a},以及圆柱体的半径 r 。
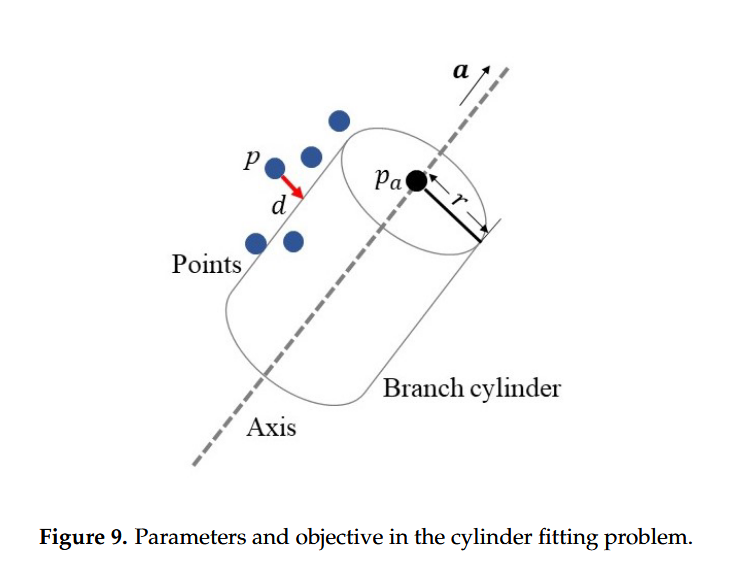
- 目标函数:各点到支圆柱的距离 d 的平方和
- 我们使用 Levenberg Marquardt (列文伯格-马夸尔特)算法来解决非线性最小二乘问题
- 它同时具有梯度法和牛顿法的优点。当λ很小时,步长等于牛顿法步长,当λ很大时,步长约等于梯度下降法的步长
- 加权优化:为了提高解的质量并减少噪声和离群点的影响,算法会重复一次最小二乘法过程 。在第二次迭代中,会为每个点分配一个权重 。这个权重是根据点在第一次拟合后与圆柱体的距离来设定的:离圆柱体表面越近的点权重越高(最高为1),越远的点权重越低(最低为0)。通过这种加权方式,可以确保拟合结果更贴近那些最能代表树干形状的核心点云
-
w_i = 1 - \frac{dist(p_i)}{dist_{max}}
-
\sum_{i=1}^{n} w_i \cdot dist(p_i)
- 其中,dist(p_i) 表示当前第 i 个点与初始计算得到的圆柱体之间的距离,dist_{max} 表示所有点到圆柱体的最大距离。之后进行归一化
- 对于小树枝,当点接近树冠和树枝顶端时会变得更加嘈杂,因此拟合精确的圆柱体是不可行的
- 我们采用异速生长法则来获得其余树枝的合理估计值。
- 一个树枝的半径与其权重成正比 。这里的权重定义为构成该树枝的两个端点顶点其子树长度的平均值
-
r_{e_i} = r_l\left(\frac{w_i}{w_l}\right)
- 其中,r_{e_i} 是第 i 个分支边缘的半径;r_l 是通过圆柱体拟合得到的树干半径;w_i 是第 i 个特定分支边缘的权重。
Adding Realism
- 这里用了这篇文章的方法Automatic reconstruction of tree skeletal structures from point clouds.来增加真实感
- 该方法基于一个观察:树木的叶子细节可以抽象为规范的几何结构,称为lobe-textures(叶瓣纹理)
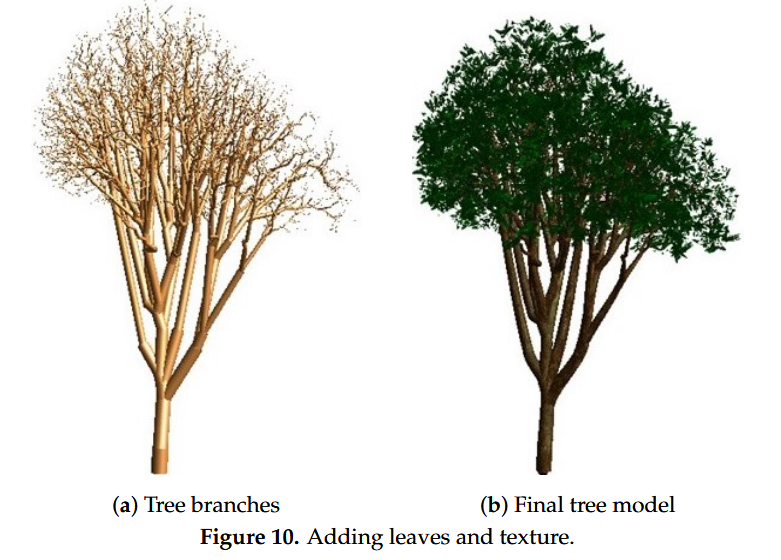
- 该方法基于一个观察:树木的叶子细节可以抽象为规范的几何结构,称为lobe-textures(叶瓣纹理)
Results and Discussion
Dataset
- publicly available point cloud repositories, the Floriade Project of Almere, and the AHN dataset
- 涵盖了静态激光扫描、移动激光扫描和机载激光扫描的范围
Visual Evaluation


- 图 11a 显示的是一棵枝干结构相对简单的垂直细长树,而图 11b 则是另一棵枝干倾斜、枝干结构复杂的树,可以看到不同类的树表现得都很好
- 可以看出,通过移动扫描(图 11c)或静态扫描(图 11d)采集的点云质量很高,因此都能准确地进行重建
- 另一方面,图 11e 给出了一个通过机载扫描获得的输入点云的例子,该输入点云的采样很差,而且相当稀疏,效果也不错
Reconstruction Accuracy
- 就单棵树而言,通常情况下,点密集度高的矮树的建模结果更为精确。此外,与形状不规则的树(如图 11b)相比,形状紧凑、标准的树通常能获得更高的重建精度。
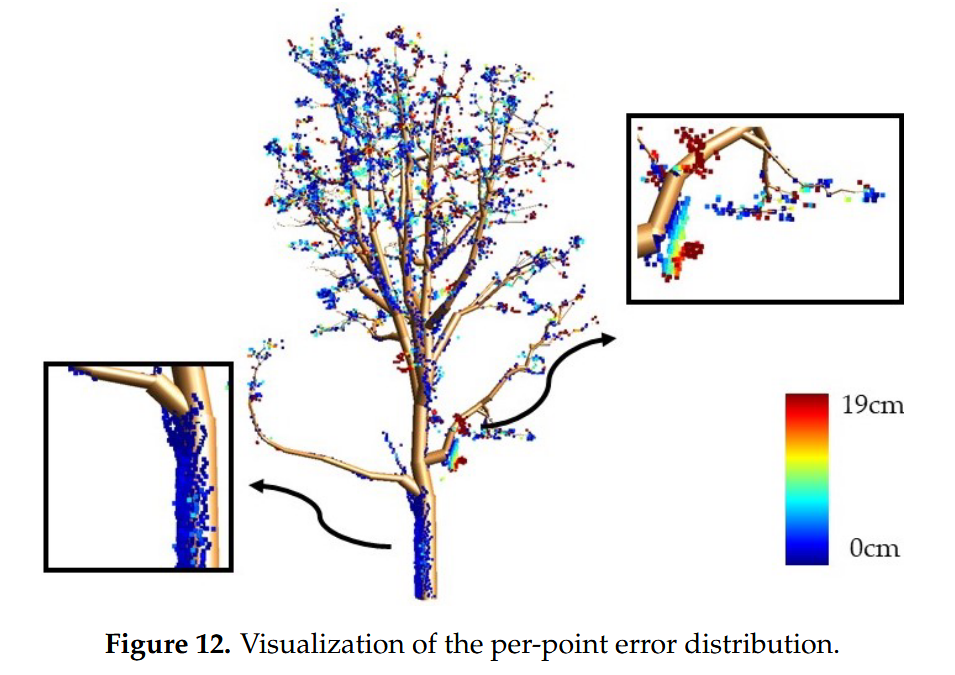
- 蓝色表示误差值小,红色表示误差值大
- 位于主枝内的点通常更接近模型,而靠近枝梢的点通常误差值较高
- 然而,分支顶端附近的点越来越少,因此不足以从采样不足的数据中可靠地重建这些小特征
Robustness
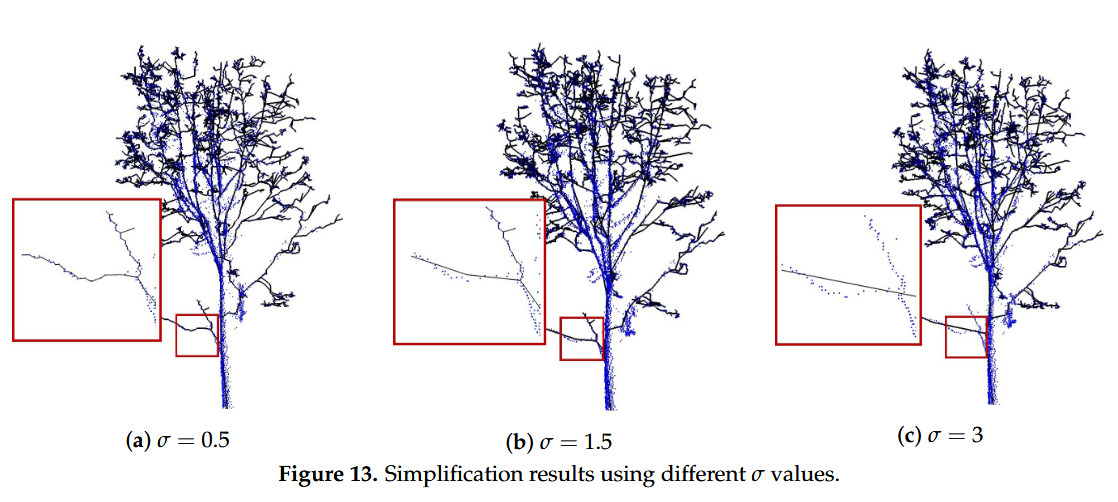
- 如果指标的 σ 临界值非常小,合并附近顶点的条件变得非常苛刻,导致骨架简化不充分,保留了过多的冗余和噪声。而如果 σ 非常大,又会导致过度简化,多重要的结构细节被错误地合并,从而丢失了树枝的自然形态。
Comparisons
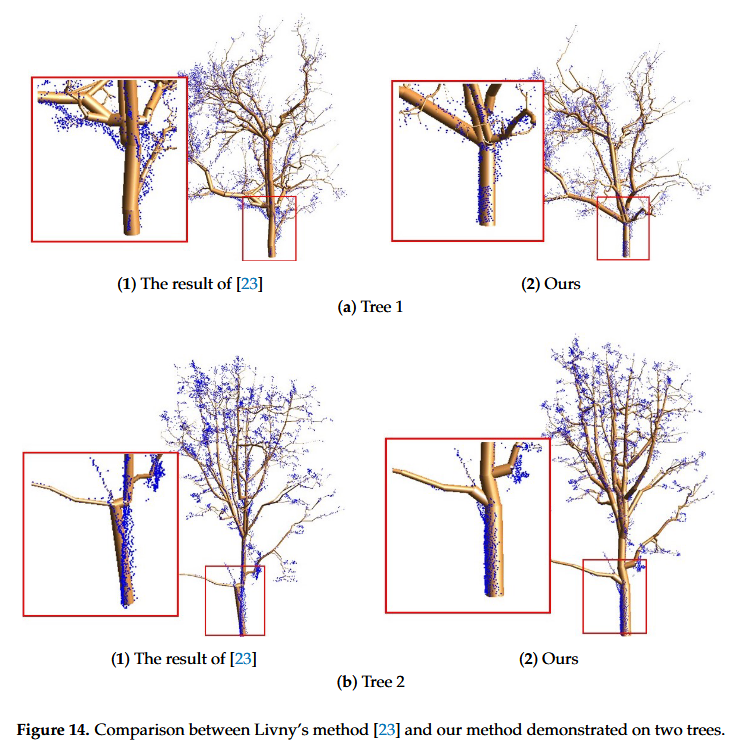
- 在点云相同的情况下,我们的算法能够重建拓扑和几何精度更高的树模型。
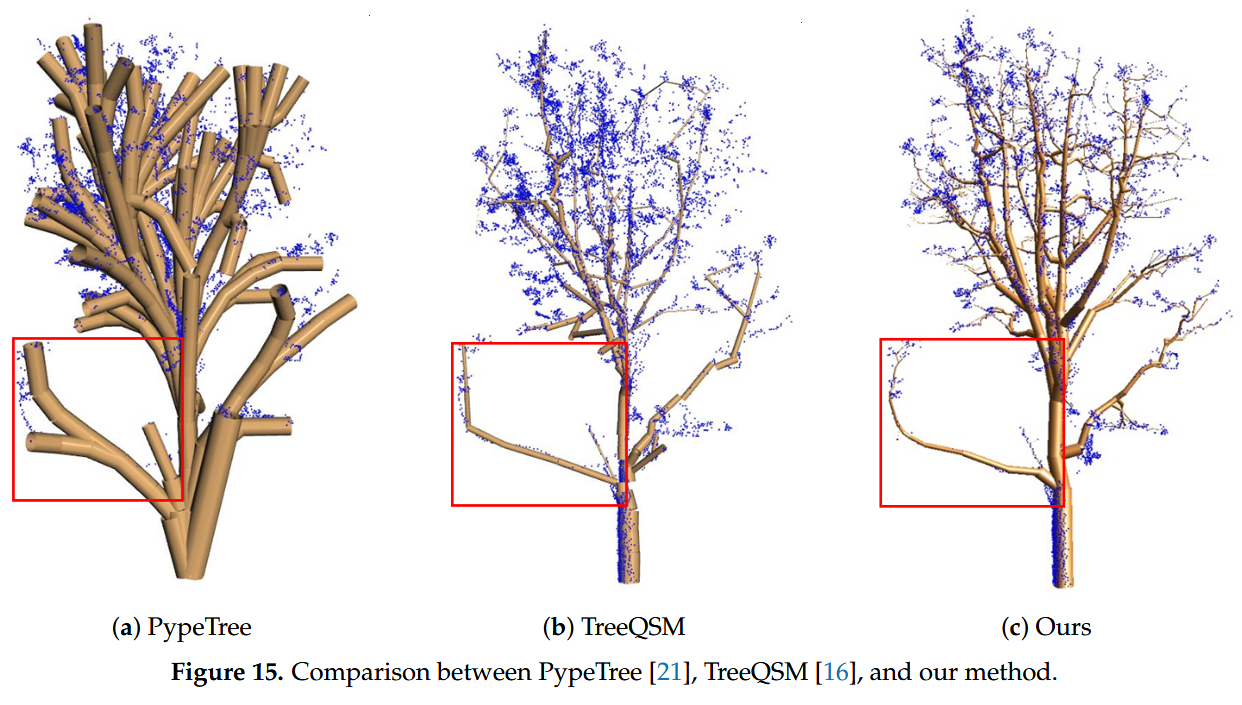
- PypeTree效果并不好,TreeQSM 无法确保树枝恢复的一致性。使用 SimpleTree 重建相当繁琐,因为它需要用户输入树枝半径等关键参数。
Limitation and future
- 对于点稀疏的低质量扫描数据,我们的方法可以重建合理的树枝拓扑结构,但无法达到足够的几何精度。此外,我们的工作没有考虑树枝的自然生长规则(如树枝分裂角度、树枝生长长度),需要领域知识
- 方法仅适用于单个树木点云,因此将现有的自动分割方法应用到我们的算法中将会扩展到更广泛的应用领域。
- 此外,由于自然界中有许多不规则形状的树枝,我们将进一步考虑拟合自由曲面,而不是圆柱体,以更精确地模拟树枝的几何形状。



评论区