本文介绍了一种为三维形状生成参数化曲面元素的方法，写的还不错，下面是我的一些理解，个人感觉和代码结合PaperRead，感受更深刻一些，所有的code来源于官方库，我也会放在评论区
Background
学习二维流形的表示
- 这里有几个专有名词我来解释一下
- 多边形网格：比如一个3D模型（比如一个球或人脸），它的表面是由很多小三角形拼接而成的，这就是多边形网格。
- 表面参数化：这是个关键概念。简单说就是把3D物体的弯曲表面"摊平"到2D平面上，就像把地球仪展开成世界地图一样。
- 当时的方法可能都有一些局限性需要进行参数化：
- 几何图像：把3D形状当作2D图像来处理
- 局部极坐标：用极坐标系来描述局部区域
- 全局无缝映射：把整个3D表面映射到2D平面
- 我们的方法可以不需要摊开，直接从原始点云数据学习，神经网络自动学会如何做参数化
深度三维形状生成
本文这段话主要讲的是用AI生成3D形状的不同方法和它们的问题：
- 非参数方法从已有的3D模型库里找最相似的，问题是必须要库里有完全一样的，不能创造新的
- 体素方法把3D空间分成小方块，用0和1表示每个方块是否有物体，虽然简单但内存消耗巨大，分辨率有限（块太大就不精细，块太小内存爆炸）
- 一些改进的方法，用八叉树（只记录有物体的区域，省内存），分层生成（先生成大部件，再细化）
- 点云方法是用一堆3D点来表示物体表面，其问题是点与点之间没有连接关系，不知道哪些点应该连成三角形，这里我们之前也有文章讲过PaperRead：A Point Set Generation Network for 3D Object Reconstruction from a Single Image
- 球面参数化方法把3D形状"摊平"到2D平面上，然后用2D网络处理，但很难找到训练数据和基础模板之间的对应关系，另外只能生成和模板拓扑相同的形状，由于生成的形状受限于模板的结构
Theoretical basis
- 这段有点过于抽象了真的看不明白（全是数学相关），我让Claude给我解释了一下，稍微清晰了一些。
- 什么是"2-流形"？在任何一点周围，都"看起来"像平坦的2D平面，就是没有"尖角"，表面光滑连续
- 什么是"图表"和"图集"？图表（Chart）：把3D表面的一小块"摊平"到2D平面的方法图集（Atlas）：很多图表的集合，覆盖整个表面，这里有点类似于分块摊平
- 为什么选择神经网络（MLP）？
命题1：局部生成正确的表面- MLP在每个小区域内都是线性变换，只要这个变换不"压扁"（满秩），就能保证生成真正的2D表面
命题2：万能近似能力 - 足够大的神经网络可以近似任何连续表面，这是神经网络的经典理论结果
- MLP在每个小区域内都是线性变换，只要这个变换不"压扁"（满秩），就能保证生成真正的2D表面
- 本文的做法：输入：2D正方形区域 [0,1]×[0,1]，神经网络把2D点映射到3D空间，让生成的3D表面尽可能接近真实表面，比较生成表面和目标表面的差异
- 这一节大概就是理论基础，感兴趣可以去看原文，因为我只是想大概了解下内容就没有太钻进去。
- 本部分的重要结论是：MLPs和ReLU构成的以 为参数的函数可以局部地实现2D点到3D surface的映射
Method
模型可以在三维形状编码的情况下解码三维曲面。这种编码可以来自许多不同的表示方法，如点云或图像。
学习解码表面
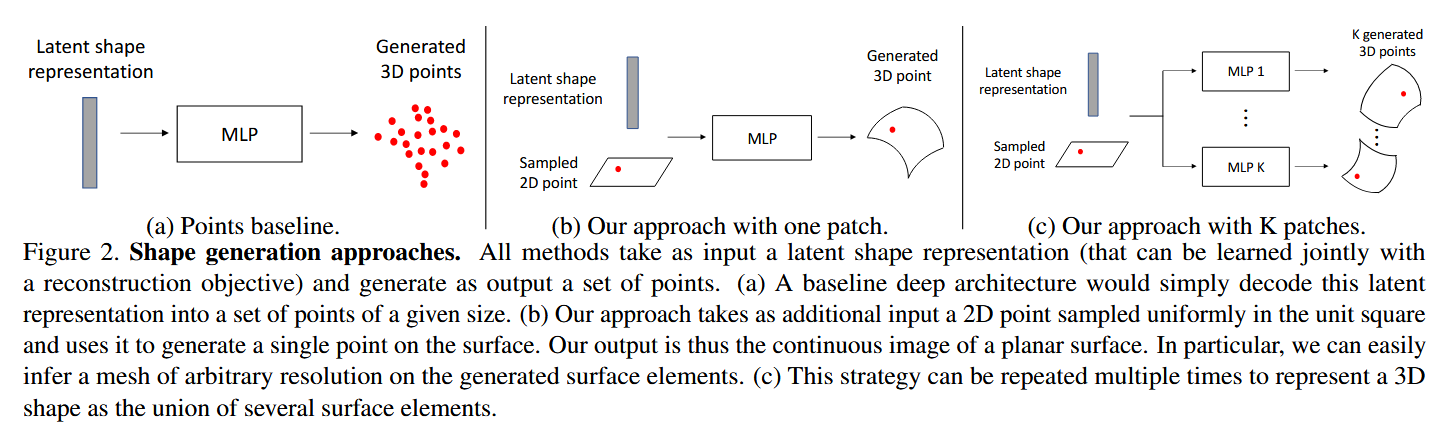
- 在理论基础部分我们也已经证明过了带有Relu的MLP可以局部地实现2D点到3D surface的映射
- 我们需要解决两个问题：(i) 如何定义生成的表面与目标表面之间的距离，以及 (ii) 如何将形状特征 x 融入到MLP中？
- 针对问题(ii)：解决方案: 将代表物体身份的形状特征
x和代表2D正方形内位置的坐标点p拼接在一起，然后将这个组合后的向量作为MLP的输入。 - 针对问题(i)：解决方案: 采用一种名为倒角损失 (Chamfer Loss) 的方法 。因为直接比较两个曲面很复杂，所以我们从生成的表面上采样一些点，再从真实的目标表面上采样一些点（记为 S∗），然后比较这两组点云的相似度 。
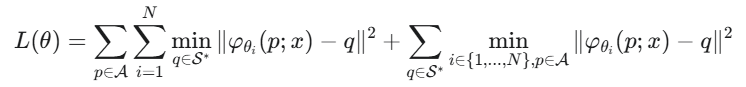这里在另一篇生成论文里有详细的解释了，这里我就不具体解释PaperRead：A Point Set Generation Network for 3D Object Reconstruction from a Single Image
实施细节
- 我们考虑两个任务：(i) 给定一个输入的三维点云，对一个三维形状进行自动编码，以及 (ii) 给定一张输入的RGB图像，重建一个三维形状。
- 编码器：我们使用了一个基于PointNet （这里有介绍PaperRead：PointNet：Deep Learning on Point Sets for 3D Classification and Segmentation）的编码器（主干网络），这个编码器（没有T-Net变换模块）将输入的点云转换成一个维度为 k=1024 的潜向量。我们实验了输入点云数量从250到2500个点不等。
# 提取1024维特征
class PointNet(nn.Module):
def __init__(self, nlatent=1024, dim_input=3):
"""
PointNet Encoder
See : PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
Charles R. Qi, Hao Su, Kaichun Mo, Leonidas J. Guibas
"""
super(PointNet, self).__init__()
self.dim_input = dim_input
self.conv1 = torch.nn.Conv1d(dim_input, 64, 1)
self.conv2 = torch.nn.Conv1d(64, 128, 1)
self.conv3 = torch.nn.Conv1d(128, nlatent, 1)
self.lin1 = nn.Linear(nlatent, nlatent)
self.lin2 = nn.Linear(nlatent, nlatent)
self.bn1 = torch.nn.BatchNorm1d(64)
self.bn2 = torch.nn.BatchNorm1d(128)
self.bn3 = torch.nn.BatchNorm1d(nlatent)
self.bn4 = torch.nn.BatchNorm1d(nlatent)
self.bn5 = torch.nn.BatchNorm1d(nlatent)
self.nlatent = nlatent
def forward(self, x):
x = F.relu(self.bn1(self.conv1(x))) # [B, 3, N] → [B, 64, N]
x = F.relu(self.bn2(self.conv2(x))) # [B, 64, N] → [B, 128, N]
x = self.bn3(self.conv3(x)) # [B, 128, N] → [B, 1024, N]
# 最大池化
x, _ = torch.max(x, 2)
#
x = x.view(-1, self.nlatent) # 重塑张量
x = F.relu(self.bn4(self.lin1(x).unsqueeze(-1))) # 第一个全连接层
x = F.relu(self.bn5(self.lin2(x.squeeze(2)).unsqueeze(-1))) # 第二个全连接层
return x.squeeze(2) # 返回 [B, 1024] 的特征向量
- 对于图像，我们使用ResNet-18作为我们的编码器。(这个在model\resnet.py)
- 解码器：4个全连接层，大小分别为1024、512、256、128，前三层使用ReLU非线性激活函数，最后一层输出层使用tanh激活函数。
# 解码
class Mapping2Dto3D(nn.Module):
"""
Core Atlasnet Function.
Takes batched points as input and run them through an MLP.
Note : the MLP is implemented as a torch.nn.Conv1d with kernels of size 1 for speed.
Note : The latent vector is added as a bias after the first layer. Note that this is strictly identical
as concatenating each input point with the latent vector but saves memory and speeed.
Author : Thibault Groueix 01.11.2019
"""
def __init__(self, opt):
self.opt = opt
self.bottleneck_size = opt.bottleneck_size
self.input_size = opt.dim_template
self.dim_output = 3
self.hidden_neurons = opt.hidden_neurons
self.num_layers = opt.num_layers
super(Mapping2Dto3D, self).__init__()
print(
f"New MLP decoder : hidden size {opt.hidden_neurons}, num_layers {opt.num_layers}, activation {opt.activation}")
# 1024、512、256、128
self.conv1 = torch.nn.Conv1d(self.input_size, self.bottleneck_size, 1)
self.conv2 = torch.nn.Conv1d(self.bottleneck_size, self.hidden_neurons, 1)
# 创建num_layers个相同的1D卷积层
self.conv_list = nn.ModuleList(
[torch.nn.Conv1d(self.hidden_neurons, self.hidden_neurons, 1) for i in range(self.num_layers)])
# hidden_neurons → 3
self.last_conv = torch.nn.Conv1d(self.hidden_neurons, self.dim_output, 1)
self.bn1 = torch.nn.BatchNorm1d(self.bottleneck_size)
self.bn2 = torch.nn.BatchNorm1d(self.hidden_neurons)
self.bn_list = nn.ModuleList([torch.nn.BatchNorm1d(self.hidden_neurons) for i in range(self.num_layers)])
self.activation = get_activation(opt.activation)
def forward(self, x, latent):
# 将第一层卷积结果与全局特征向量相加
x = self.conv1(x) + latent
x = self.activation(self.bn1(x))
x = self.activation(self.bn2(self.conv2(x)))
for i in range(self.opt.num_layers):
x = self.activation(self.bn_list[i](self.conv_list[i](x)))
return self.last_conv(x)
def forward(self, latent_vector, train=True):
"""
Deform points from self.template using the embedding latent_vector
:param latent_vector: an opt.bottleneck size vector encoding a 3D shape or an image. size : batch, bottleneck
:return: A deformed pointcloud os size : batch, nb_prim, num_point, 3
"""
# Sample points in the patches
# input_points = [self.template[i].get_regular_points(self.nb_pts_in_primitive,
# device=latent_vector.device)
# for i in range(self.opt.nb_primitives)]
if train:
# 这行代码正在为每一个“面片”（primitive）生成一组随机的起始坐标点，数量是每个面片需要的点数，并将它们收集到一个列表中。
input_points = [self.template[i].get_random_points(
torch.Size((1, self.template[i].dim, self.nb_pts_in_primitive)),
latent_vector.device) for i in range(self.opt.nb_primitives)]
else:
input_points = [self.template[i].get_regular_points(self.nb_pts_in_primitive_eval,
device=latent_vector.device)
for i in range(self.opt.nb_primitives)]
# [batch_size, nb_primitives, 3, num_points]
# Deform each patch，拼接之后解码，再把面片按照规则拼接起来
# 最后把所有片段组装起来
# 完整雕塑 = [片段0, 片段1, 片段2]
output_points = torch.cat([self.decoder[i](input_points[i], latent_vector.unsqueeze(2)).unsqueeze(1) for i in
range(0, self.opt.nb_primitives)], dim=1)
# Return the deformed pointcloud
return output_points.contiguous() # batch, nb_prim, num_point, 3
- 我们训练时总是使用在所有可学习参数化上均匀采样的2500个输出点（这里代码中会有球形网格和正方形网格，这里指定数量的生成网络（顶点和面片方式的代码部分我个人觉得值得深究）（就是他会根据点数来定义网格））（代码在model\template.py），因为chamfer loss会与输入点的数量成平方关系，在每个训练步骤中，都会重新对可学习的参数化以及地面真实点云进行采样，以避免过拟合。
- 在训练单视图重建任务时，我们发现通过使用来自点云自动编码器的解码器并固定其参数，只训练编码器，可以获得最好的结果。
- 最后，我们注意到在可学习的参数化上，从一个规则的网格上采样点比随机采样点能产生更好的性能。所有的结果都使用了这种规则采样。
网格生成
我们已经拿到了每个面片的点，我们怎么把每个面片进行拼接呢？
将面片网格的边传播到三维点上（code中用的是这个）
2D正方形网格 → 应用学习的映射 → 3D表面网格
- 优势
- 高分辨率：可以生成非常精细的网格（22500个点）
- 内存效率：点可以分批处理，避免内存问题
- 速度快：直接映射，无需额外计算
- 缺陷
- 不封闭：网格可能有开口
- 有洞：不同patch之间可能有小间隙
- 重叠：不同patch可能相互重叠
def generate_mesh(self, latent_vector):
assert latent_vector.size(0)==1, "input should have batch size 1!"
import pymesh
# 在2D模板上创建规则网格（如均匀分布的网格点）
input_points = [self.template[i].get_regular_points(self.nb_pts_in_primitive, latent_vector.device)
for i in range(self.opt.nb_primitives)]
# 在2D模板上创建规则网格（如均匀分布的网格点）
input_points = [input_points[i] for i in range(self.opt.nb_primitives)]
# Deform each patch
# [batch_size, nb_primitives, 3, num_points]
# Deform each patch，拼接之后解码输出生成的点的坐标
output_points = [self.decoder[i](input_points[i], latent_vector.unsqueeze(2)).squeeze() for i in
range(0, self.opt.nb_primitives)]
# 使用原始2D模板的面片连接信息，根据输出的顶点坐标和面片信息创建3D网格
output_meshes = [pymesh.form_mesh(vertices=output_points[i].transpose(1, 0).contiguous().cpu().numpy(),
faces=self.template[i].mesh.faces)
for i in range(self.opt.nb_primitives)]
# Deform return the deformed pointcloud
# 将所有primitive的网格合并成一个完整网格
mesh = pymesh.merge_meshes(output_meshes)
return mesh
生成一个高密度的点云并使用泊松表面重建（PSR）
- 注：这个这篇文章的code没有用到，我就单独翻译一下
- 为避免前面提到的缺点，我们可以额外地对表面进行密集采样，并使用一种网格重建算法。我们首先如上所述，生成一个高分辨率的表面。然后我们从无穷远处向模型发射光线，获得大约100000个点及其带方向的法线，接着就可以使用像PSR这样的标准带方向点云重建算法来生成一个三角形网格。我们发现，高质量的法线和高密度的点云对PSR的成功至关重要，而这些都可以通过我们的方法自然地获得。
在封闭表面上而不是在面片上采样点
- 为了从我们的方法中直接获得一个封闭的网格，而无需上述的PSR步骤，我们可以从一个三维球体的表面而不是二维正方形上采样输入点。该方法的质量取决于底层表面能被一个球体表示得有多好。
总结一下
- 输入的如果是点云用Pointnet编码，如果是图片用ResNet编码
- 解码就用的是很多全连接层和激活函数，这里的输入包括编码，以及正方形或者圆形的采样点坐标，其中在第一层卷积结果与全局特征向量相加
- 之后每个面片都会输出点的坐标信息
- 如何连接？通过我们当时划分面片时的连接方式，按照原来的方式再连接到一起
Experiment
- 数据：我们在标准的ShapeNet Core数据集(v2)上评估了我们的方法 。
- 评估标准：CD，还有METRO软件
自动编码三维形状
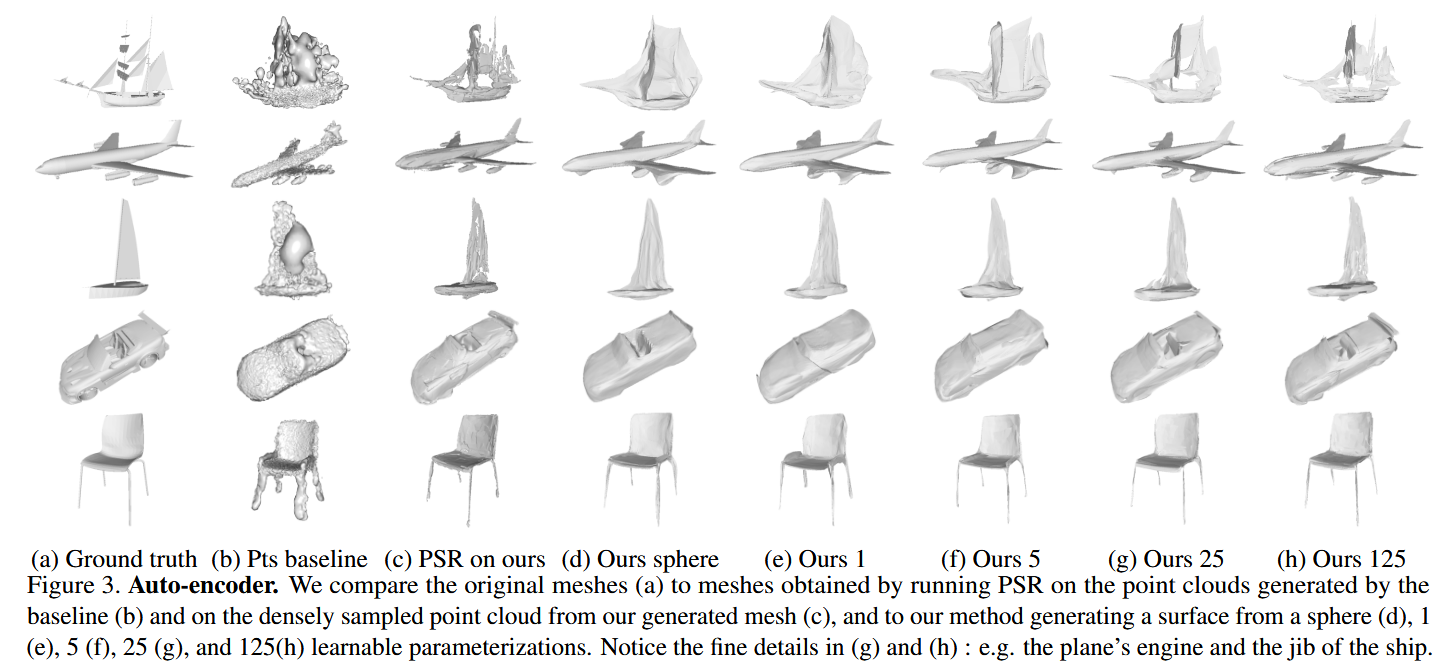
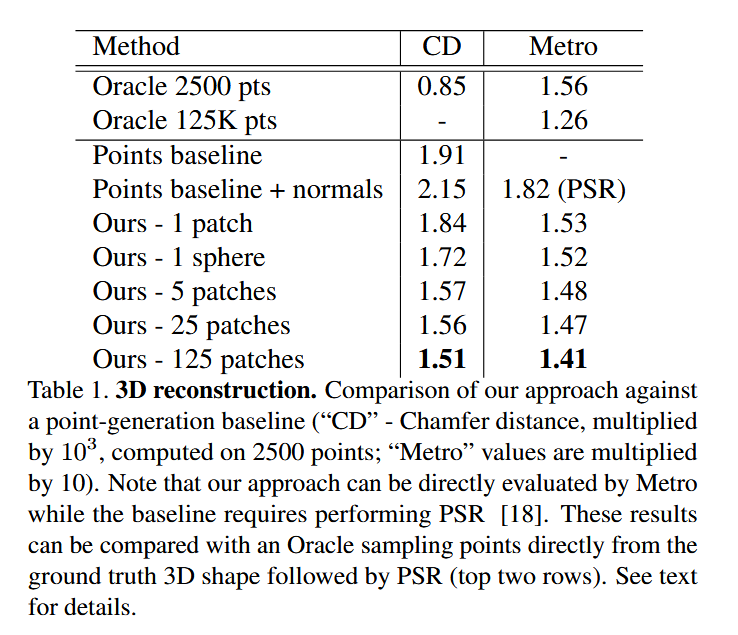
- AtlasNet完胜: 无论是在点云相似度(CD)还是网格质量(Metro)上，AtlasNet都全面优于简单粗暴的“点基准”模型 。
- 面片越多越好: 随着面片数量从1增加到125，生成模型的质量越来越高，能捕捉到更多细节，如飞机的引擎
- 球体 vs. 面片: 使用单个球体作为模板，效果比单个面片好，但不如多个面片组合
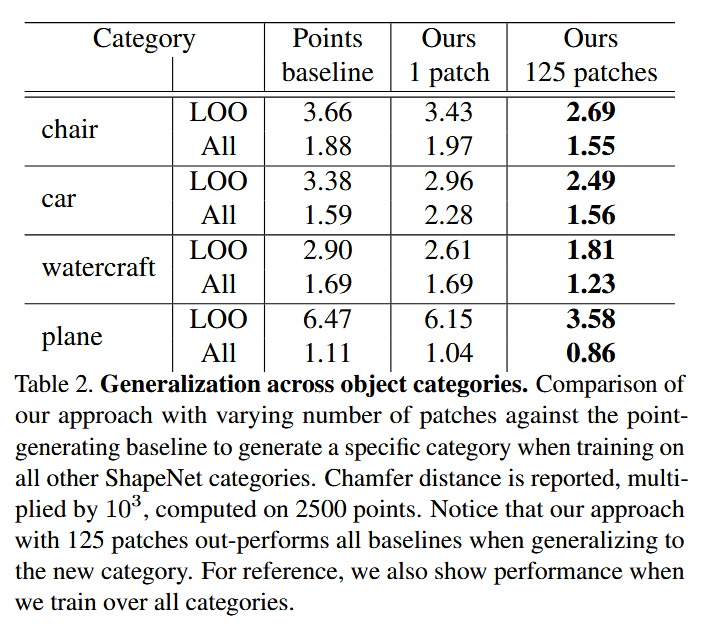
- 泛化能力 :
- 实验: 做一个“留一法”测试，比如训练时不让模型看任何“椅子”，然后测试它重建椅子的能力 。
- 结果: AtlasNet的泛化能力同样强于基准模型 。但结果也显示，没见过的东西确实做得不好，比如没见过椅子的模型，生成的椅子腿和扶手就很模糊，因为它不知道这种细长结构是什么
单视图重建
- 任务: 输入一张2D图片，重建3D模型 。
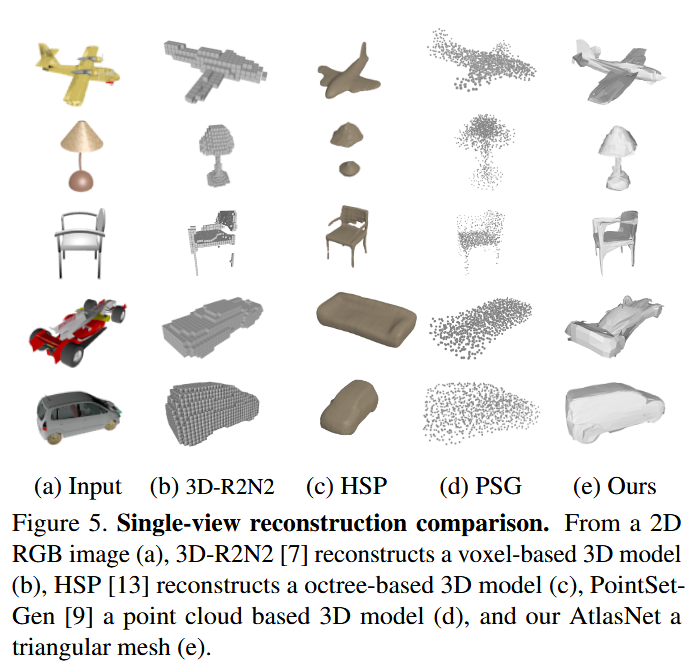
- 定性对比:
- 输出形式多样: AtlasNet直接生成网格，而其他方法生成的是体素（像乐高积木）或点云 。
- 细节更丰富: AtlasNet的网格能展现其他方法难以表达的精细表面细节 。
- 只生成表面: AtlasNet只在物体表面生成点，而有的方法会在物体内部也生成一些“废点” 。
- 定量对比 (表3, 4):
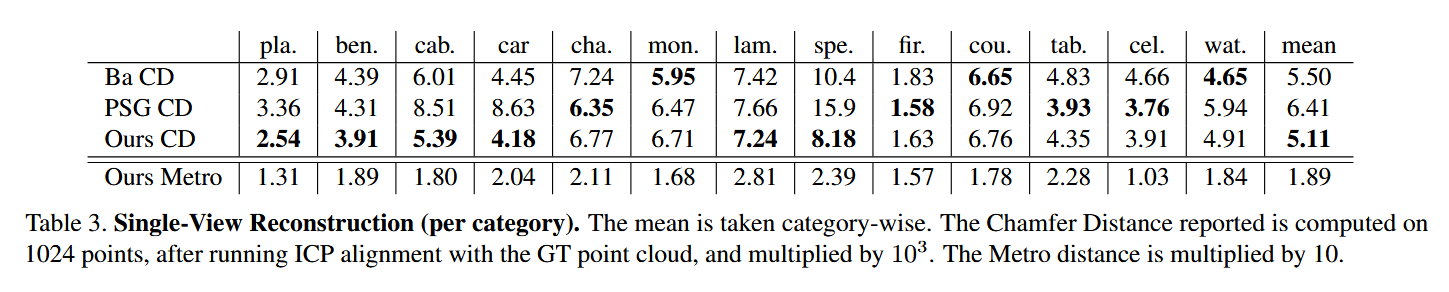
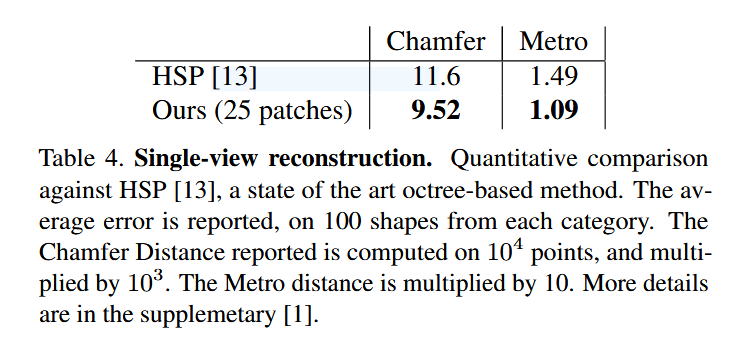
- 全面领先: 与其他SOTA（state-of-the-art）方法（如PointSetGen, HSP）相比，经过公平的对齐和重训练后，AtlasNet在多个类别上和平均性能上都取得了更好的或有竞争力的结果 。
附加应用
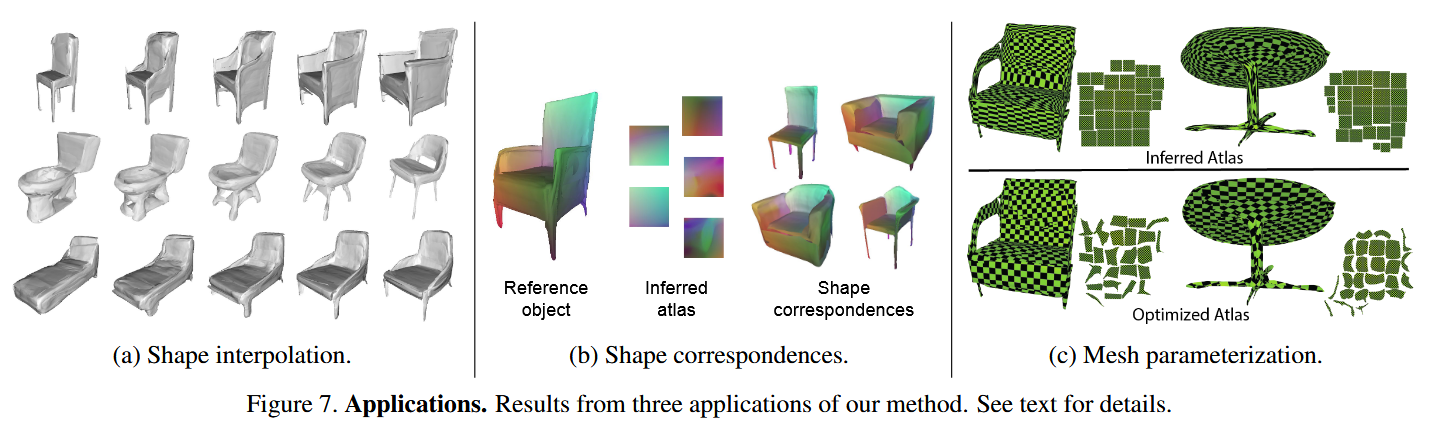
- 形状插值 (图7a): 由于AtlasNet将每个形状都编码成了一个向量，我们可以在两个形状的向量之间进行线性插值。解码这些中间向量，就能得到两个形状之间平滑、自然的渐变过程，比如一把椅子慢慢“长出”扶手 。
- 形状对应 (图7b): 这是AtlasNet最神奇的应用之一。因为它用同一组“图集”（25个正方形）去构建所有椅子，所以每个正方形上的同一点（比如左上角点），在所有椅子上对应的3D位置，会被认为是“对应点”。结果是，模型自动地找到了所有椅子椅背对应椅背、椅腿对应椅腿的关系，而这一切都无需任何人工标注 。
- 网格参数化 (图7c): 模型直接生成的UV图（用于贴图）质量不高，有很大拉伸 。但因为每个面片都是简单的拓扑结构，所以可以非常容易地用现有工具进行优化，得到一个高质量的UV图，方便进行纹理贴图 。
Conclusion
本文介绍了一种为三维形状生成参数化曲面元素的方法，展示了这种方法在三维形状和单视角重建方面的优势，其性能优于现有的基线方法。此外，还展示了它在形状插值、查找形状对应关系和网格参数化方面的前景。该方法为三维形状的网格生成和合成开辟了应用领域，类似于静态图像生成。
评论区